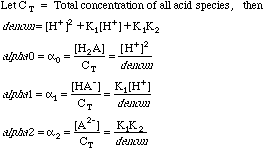
Advanced Methods Tutorial 01
Solubility Product Problems

If you have ever been exposed to the numerical methods used to solve for the roots of equations, you will have learned that you can make some terrible blunders by blindly using these programs. Fortunately, as Chemists, we can guide these programs by suggesting to them where they should look for solutions. To do this, we must first be familiar with the simple approximations learned in freshman chemistry or from my Survival Guide to Analytical Chemistry. We should also have an intuitive feel for things like pH.

Thinking Like a Chemist

What is the pH of a saturated solution of CaC₂O₄ (calcium oxalate)? Ksp of calcium oxalate is 1.7x10^-9.

Student: How should I know? That's what we are tying to calculate here. Where is the formula to compute this?

Professor: Forget formulas. Close your eyes. Feel the Force. (Sorry, the Star Wars re-release is in the theaters at the moment.) Is it 3?

Student: Uh, lets see. When we put CaC₂O₄ in water we will get a little calcium ion and a little oxalate ion. Oxalate ion is the salt of oxalic acid. Salts of weak acids are bases. At these low concentrations I doubt that calcium ion will exhibit much acidic behavior. It should probably be a little basic, so pH of 3 is out.

Professor: Very good Grasshopper (for all you Kung Fu fans). How about a pH of 10?

Student: It won't be that basic. The concentrations will be very low. Calcium oxalate is only slightly soluble, that's why we are doing a Ksp problem using it. I would guess very slightly basic, probably between 7 and 8.

Professor: You have chosen wisely. (Quick, which Indiana Jones movie did THAT come from?)

On to the Advanced Solution:

Our problem is to compute the concentration of calcium ion in a saturated solution of calcium oxalate.

First we must do some more thinking like chemists.

When we put calcium oxalate into water it will first dissociate in the classic Ksp manner:

But oxalate is one of the salts of the polyprotic acid H₂C₂O₄, so it will further split into some combination of H₂C₂O₄, HC₂O₄^-, and C₂O₄^2-. We have learned elsewhere that the concentrations of each of these species can be calculated using the Fraction of Species equations, which are messy polynomials made up from [H⁺], and the diprotic acid dissociation constants K₁, and K₂. We dealt with these before when we used a spreadsheet to calculate the so-called alphas of a diprotic acid for a large range of pH's.

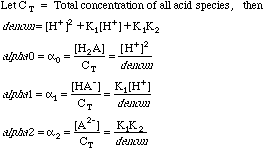
We know that given the pH and the K₁ and K₂ we can generate any alpha when we need it, so consider the alphas as a solved problem.

The only real trick needed to solve our Ksp problem is to remember that if CaC₂O₄ has been put into pure water, then

This so-called Mass Balance expression is not entirely obvious, but is true given the conditions specified in the problem. Just remember: We are Professionals. We know things like this. People will pay fat consulting fees to have us solve problems of this complexity.

As chemistry majors we have had at least three semesters of advanced mathematics. The math that follows looks messy but is just simple algebra.

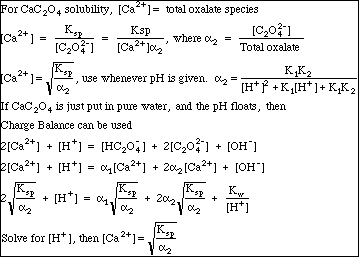
Note the Charge Balance expression. Remember that setting up Charge Balance is always easy. Just make a list of all ions in solution, put the positive ones (the cations) on the left, and the negative ones (the anions) on the right. Multiply each concentration by the ion charge. That's it.

Now for the Brute Force spreadsheet solution using Microsoft Excel 5.0. You may need to scroll around to see all parts of this if you are viewing this document on a Web page:

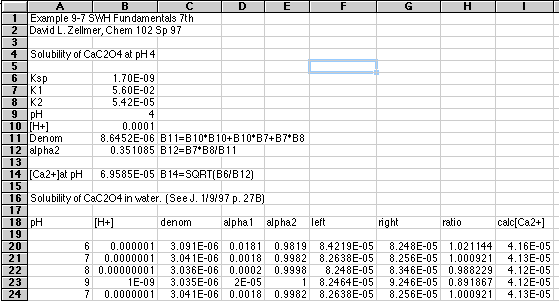
In row 14 we first tested our equations by computing [Ca²⁺] at a given pH, using the equation

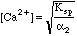
Starting in row 18 we generalized to the situation where the pH "floats," reaching whatever value it will have when equilibrium is reached. Spreadsheet equations are used to compute all the alphas, and the right and left sides of the general equation. When left=right we will know the pH needed to make the equation true. We can then calculate [Ca2+] from Ksp and the value of alpha2 at this pH using the equation above.

As we expected, the ratio between left and right shifted to 1.000 somewhere between pH 7 and 8. We can refine this further by specifying a more closely spaced set of pH's:

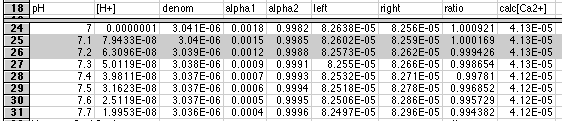
Now we see that the solution lies between pH 7.1 and 7.2. Our spreadsheet has computed a value of [Ca²⁺] of 4.13x10^-5 at both pH's, so we have our solution.

For a more elegant way of solving this equation, use Goal Seek:

The last two rows (33 and 35) illustrate the use of the Goal Seek... tool found under the Tools menu. Our goal is to make the left and right sides the same. Two cells are involved. Example: Cell H33 contains the ratio between left and right. Our goal is to make this ratio = 1.000. Cell A33 has a value (not a formula) somewhere near what we expect to work. In this example I started with a value of 7 in this cell. (Remember, as Chemists, we expect the final pH to be between 7 and 8.) Select cell H33. Choose Goal Seek... from the Tools menu. A dialog box asks you the cell to change and the value to seek. Enter A33 for the cell, and 1 for the goal. Click OK. The program will iterate until the goal is reached +or- 0.001. A33 displays the final value. In my example, the solution to the problem appears in cell I33.Pretty neat, huh?

Note that using a difference instead of a ratio will not work with most equilibrium problems because the values are too small. That's why I went to a ratio. Use of pH as the varied parameter was probably necessary also, since values have to look like dollars to get this business-oriented program to work on it. Varying values around 1E-07 would probably not work with this program. Goal Seek is simple, and does not let you change either the error value (0.001) or the number of iterations (probably 100). Even so, this worked quite well and was very easy to do. It was somewhat in error because of its 0.001 error limit. The true pH should have been between 7.1 and 7.2, but Goal Seek stopped at 7.094. The final value for [Ca2+] was well within the significance needed for the problem, however. A practical way to do this (with good instructional goals as well) is to do a rough search for solutions at full pH values. Then pick the nearest pH that might work and use Goal Seek... on it. This should give you a feel for how the system responds to pH (or other parameter).

For more control over the iteration process, you can set up a formula with a circular reference, then under Tools/Options... find the Calculate Tab, where you can set the number of iterations and the allowed precision. You also tell Excel that the cell in question is authorized for circular references.If we ever need to use this I will explain the concept of the circular reference at a later date.

Finally, the Big Kahuna is the Solver. This add-in tool in Excel 5.0 lets you vary up to 200 cells to seek a final goal. This might be fun to try on something really complicated.

You can also use advanced mathematics programs such as Mathematica on this. Be advised, however, that a simple-seeming request to solve for the roots of the expression you generate may produce nonsensical values unless you guide the process with your chemical knowledge.

Challenge Problem:

Since each term in our left = right equation stands for one of the ions in solution, we should be able to compute the Ionic Strength. From the Ionic Strength we can compute the activity coefficients of all the ions in our equilibrium expressions, then correct all the equilibrium constants to their real values. Now recompute the solution to the problem. Some circular references will occur, but Excel can be told to proceed to a solution anyway.