
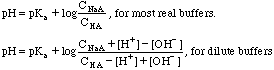
1. Compute pH given the actual concentrations of the conjugate acid and conjugate base.
The pH is easily calculated with:

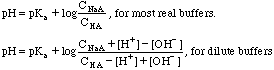
2. The pH shift problem:
If you add 2.00 mL of 0.100 M HCl to 100 mL of a buffer consisting of 0.100 M HA and 0.200 M NaA, what will be the change in pH?
Ka of HA is 1.5x10-5. pKa = 4.82.
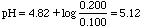
If we add a strong acid to a weak base, such as NaA, they REACT and form new products.
(The total ionic equation is H+ + Cl- + Na+ + A- --> HA + Na+ + Cl-)
mmoles HCl
|
mmoles
HA
|
mmoles
NaA
|
Volume,
mL
| |
| Initial
|
0.200
|
10.0
|
20.0
|
100+2
mL
|
| Final
|
0
|
10.2
|
19.8
|
102
mL
|
| Molarities
|
10.2/102
|
19.8/102
|
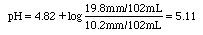
3. The "make a buffer of given pH" problem:
We wish to prepare a buffer of pH 10 using common laboratory reagents. How many mL of 6M HCl would we have to add to a solution prepared by adding 100 mL of 15M NH3 to 200 mL of water?
Ka of NH4+ = 5.70x10-10, pKa = 9.24.
mmoles HCl
|
mmoles
NH4Cl
|
mmoles
NH3
|
Volume
| |
| Initial
|
x
|
0
|
1500
|
x/6M
+ 300mL
|
| Final
|
0
|
x
|
1500-x
|
x/6M
+ 300mL
|
| Molarity
|
We didn't bother computing the molarities, since the volumes cancel out in the buffer equation anyway--a good thing, since the volumes have an "x" in them.
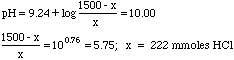
Finally, 222 mmoles HCl/6M = 37.0 mL of 6M HCl needed.
Note that the buffer produced will not actually have a pH of 10. The concentrations are so high that we would need to compute activities from the ionic strengths and generate a corrected value of the Ka for ammonium ion. In an actual lab, we would make up the buffer as calculated above, then use a pH meter and HCl or NH3 to adjust the buffer to 10.0.