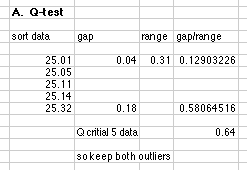
1. The following results were obtained from the calibration of a 25.00 mL pipet: 25.05, 25.14, 25.01, 25.11, 25.32 mL.
A. Using the Q-test, should any of the values be thrown out before we do further analysis?

B. Using all acceptable values that remain, compute the mean, standard deviation, and 95% confidence limit for these values. Also compute the relative error in %, using the confidence limit as your absolute error.
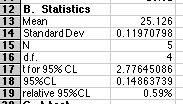
C. Use a t-test to determine if the mean value is significantly different from 25.00. Explain your reasoning.

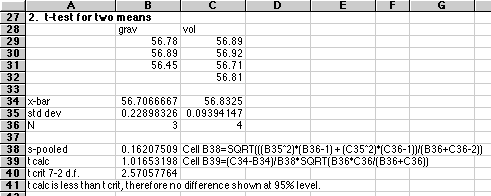
2. Two methods were used on the same unknown. Gravimetric gave 56.78, 56.89, and 56.45 %Cl. Volumetric gave 56.89, 56.92, 56.71, and 56.81 %Cl. Are these two means significantly different? Explain your reasoning.
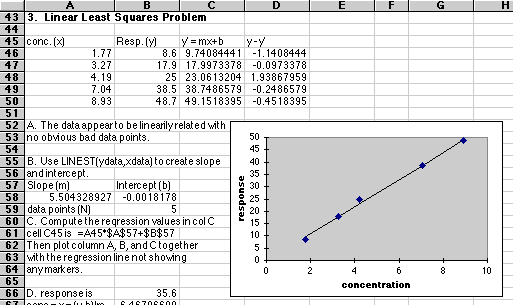
| Concentration,
mg/L
|
Response
(Arbitrary Units)
|
| 1.77
|
8.6
|
| 3.27
|
17.9
|
| 4.19
|
25.0
|
| 7.04
|
38.5
|
| 8.93
|
48.7
|
A. Plot these data. Are these data suitable for Least Squares Analysis?
B. Compute the slope and intercept for the line.
C. Plot the least squares line through the data.
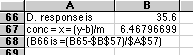
E. "By hand" draw in possible upper limits and lower limits to possible other lines through the data. You can use these lines to estimate the errors about the line. Estimate the error in the computed concentration in (D).
Since I was using my computer and didn't have a printer handy so that I could draw lines "by hand" I did something equivalent -- I estimated the errors by looking at the computed differences between the regression line and the data. Remember that the X-error is just the Y-error divided by the slope.

F. Compute the 95% Confidence Limits for the concentration in (D). [Hint: Look at the equations in the Statistics Handouts and in SWH. Some versions of Excel will supply you with Sy/x.] Compare this computed value with that estimated in (E).
