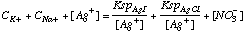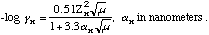Ionic strength (mu) = 2.29E-02.Solubility Product
Feb 26, 1997 Name ____________________________
1. 0.5143 g of Ag2CrO4 is placed in 104.3 mL of water. Ksp of silver chromate is 1.2 x 10-12.
A. Calculate the concentrations of Ag+ and of CrO42-.
Simple solubility. [Ag+] = 2[CrO42-]; [Ag+]2[CrO42-] = Ksp; let s = [CrO42-]
then (2s)2(s) = Ksp; s = (Ksp/4)1/3 = 6.6943E-05 (note: this is computer talk for 6.69 x 10-5). Since chromate = s = 6.6943E-05, then [Ag+] = 2[CrO42-] = 1.34E-04
B. Calculate how many grams of silver chromate have dissolved.
6.6943E-05
|
moles
silver chromate
|
0.1043
|
liter
|
331.73
|
g
Ag2CrO4
|
| liter
|
mole
| ||||
| equals
|
2.32E-03
g
|
2. 0.5143 g of Ag2CrO4 is placed in 104.3 mL of 0.02 M Ag+. Ksp of silver chromate is 1.2 x 10-12.
A. Calculate the concentrations of Ag+ and of CrO42-.
This is a common ion problem. To a first approximation we can just plug the 0.02 M Ag+ concentration into the Ksp expression and solve for chromate. Since Ag+ is in excess, s = moles of silver chromate that have dissolved per liter = [CrO42-]
[Ag+]2[CrO42-] = Ksp (0.02)2[CrO42-] = Ksp [CrO42-] = (1.2E-12)/(0.02)^2 = 3.00E-09 M. [Ag+] = 0.02 M to a first approximation, at least. Adding 2x3.00E-09 to 0.02 will not change its value significantly. (This would be the approximate concentration of silver ion generated by the dissolution of the silver chromate.)
B. Calculate how many grams of silver chromate have dissolved.
3.00E-09
|
moles
silver chromate
|
0.1043
|
liter
|
331.73
|
g
Ag2CrO4
|
| liter
|
mole
| ||||
| equals
|
1.04E-07
g
|
3. 1.23 millimoles of KI, 2.21 millimoles of NaCl, and 2.04 millimoles of AgNO3 are mixed together in 150 mL of solution. Ksp AgCl is 1.8 x 10-10, Ksp AgI is 8.3 x 10-17.
A. Set up an Initial/Final Spreadsheet and calculate how many millimoles of each ion (and AgI and AgCl solids) are found in the final solution.
K+
|
I-
|
Na+
|
Cl-
|
Ag+
|
NO3-
|
AgI(s)
|
AgCl(s)
|
Volume
| |
| Initial
|
1.23
|
1.23
|
2.21
|
2.21
|
2.04
|
2.04
|
0
|
0
|
150
mL
|
| Semifinal
|
1.23
|
~0
|
2.21
|
2.21
|
0.81
|
2.04
|
1.23
|
0
|
|
| Final
|
1.23
|
~0
|
2.21
|
1.40
|
~0
|
2.04
|
1.23
|
0.81
|
150
mL
|
| Conc.
|
1.23mm/150mL
= 8.20E-03 M
|
see
(2) below
|
2.21/150=
1.47E-02 M
|
1.40/150 =
9.33E-03 M
|
see
(1)
below
|
2.04/150 =
1.36E-03 M
|
(1) [Ag+] = KspAgCl/[Cl-] ~ 1.8E-10/9.33E-03 = 1.93E-08 M
then plugging this value into the Ksp for AgI we get
(2) [I-] = KspAgI/[Ag+] ~ 8.3E-17/1.93E-08 = 4.30E-09 M
B. Compute the concentrations of each ion in solution. (Ag+, K+, Na+, Cl-, I-, NO3-). For most of these the calculations should be straightforward. If it looks like the usual approximations won't work, see F and G below for the general approach to be used.
The concentration calculations are given in the last row of the answer to part A.
C. Compute the ionic strength (greek letter mu) of this solution. (computer notation used)
mu= 0.5SUMCiZi2 = 0.5(8.20E-03*(+1)^2 + 4.30E-09*(-1)^2 + 1.47E-02*(+1)^2 + 9.33E-03*(-1)^2 + 1.93E-08*(+1)^2 + 1.36E-02*(-1)^2) = 2.29E-02 M
D. Compute the activity coefficients for Ag+, Cl-, and I-.
Using the equations found in SWH, 7th edition:
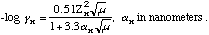Ionic strength (mu) = 2.29E-02.
alpha Ag+ = 0.25 nm, alpha Cl- = 0.3 nm, alpha I- = 0.3 nm. Plug in and calculate activity coefficients (Greek letter gamma). I got gamma Ag+ = 0.854, gamma Cl- = 0.857, gamma I- = 0.857
E. Compute corrected Ksp's for AgCl and for AgI
Ksp AgCl = [gamma]Ag+[Ag+][gamma]Cl-[Cl-]; Ksp'AgCl = F(KspAgCl,([gamma]Ag+)([gamma]Cl-))
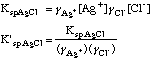
= 1.8E-10/(0.854*0.857) = 2.46E-10;
Calculate Ksp'AgI in the same way and get 1.13E-16
F. Write a charge balance expression for this mixture.
[K+] + [Na+] + [Ag+] = [I-] + [Cl-] + [NO3-]
G. Plug in the appropriate expressions to create a polynomial in which [Ag+] is the only unknown.
