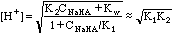
In-Class Problem Set #4 Answer Sheet
Acid and Base Calculations
15 March 1996 Name: _____________________________
The following table of acid dissociation constants may prove useful: (Spreadsheet notation is used in place of Scientific notation; e.g. 1.75 x 10-5 appears as 1.75E-05.) Remember, your book does not list Kb's, even when the name of the compound is that of the weak base form.
Name
|
K1
(or Ka)
|
K2
|
K3
|
K4
|
| Acetic
acid
|
1.75E-05
|
|||
| Ammonia
|
5.70E-10
|
|||
| Arsenic
acid (H3AsO4)
|
5.8E-03
|
1.10E-07
|
3.2E-12
|
|
| Benzoic
acid
|
6.8E-05
|
|||
| Benzylamine
|
4.5E-10
|
|||
| Carbonic
acid
|
4.45E-07
|
4.69E-11
|
||
| Phthalic
acid
|
1.12E-03
|
3.90E-06
|
The amphiprotic equation which none of us ever remembers is:
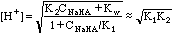
1. Categorize each of the following as SA (strong acid), SB (strong base), WA (monoprotic weak acid), WB (monoprotic weak base), Buffer (either monoprotic or polyprotic), Amphiprotic, WA but polyprotic, WB but polyprotic, or Needs Advanced Computer Solution Even to Get Close (NACS).
In the case of the polyprotic WA and WB, we can usually use the monoprotic approximation; but if we can't, then classify it as NACS. Some mixtures of things may react (Initial/Final Spreadsheet time!) to form new products that fall into a familiar category, such as a buffer, or a large excess of SA or SB that controls the pH. But some mixtures are just plain weird. In these cases, state what the final mixture is composed of, then categorize it as NACS. The normal iterative or quadratic equation methods we have learned for very dilute strong acids and bases, or for some of the WA and WB problems we have done are methods you are supposed to know and are not to be classified as NACS.
A. 0.001 M sodium acetate
Weak base (salt of weak acid)
B. carbon dioxide dissolved in water
Polyprotic Weak Acid (H2CO3)
C. 0.1 M potassium hydrogen phthalate ("KHP")
Amphiprotic
D. 1.5E-08 M nitric acid
Strong Acid
E. A solution 0.1 M in acetic acid and 0.3 M in sodium acetate
Buffer
F. 30.0 mL of 0.100 M ammonia is mixed with 20.0 mL of 0.050 M HCl
3 mm NH3 (weak base) + 1 mm HCl (strong acid) --> 2 mm NH3 (weak base) + 1 mm NH4+ (conjugate weak acid). This makes a buffer. (mm = millimoles)
G. 30.0 mL of 0.100 M ammonia is mixed with 40.0 mL of 0.100 M HCl
3 mm NH3 (weak base) + 4 mm HCl (strong acid) --> 3 mm NH4+ (weak acid) + 1 mm HCl (strong acid). The 1 mm of HCl will likely dominate the pH, making this a Srong Acid approximation. To include the possible effect of the NH4+ we would need an advanced solution.
H. 10.0 mL of 0.100 M ammonia is mixed with 20.0 mL of 0.010 M Na3AsO4
This is a mixture of 1.0 mm of NH3 (weak base) with 0.2 mm of Na3AsO4 (a different weak base). Kb's of these (Kb = Kw/Ka) are 1.75E-05 and 3.1E-03, respectively. It is not clear that either of these will dominate the pH, although the Na3AsO4 has the best crack at it. It is best to designate this one as NACS, needing an Advanced Solution.
2. Solve for the pH of parts A, C, F, and G above. (Add 2.I. below)
A. 0.001 M sodium acetate
Weak Base, so use
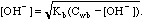
Kb = Kw/Ka = 1E-14/1.75E-05 = 5.71E-10.
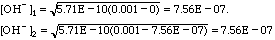
so good enough. pOH = -log(7.56E-07) = 9.12; pH = 14 - 9.12 = 7.88.
C. 0.1 M potassium hydrogen phthalate ("KHP")
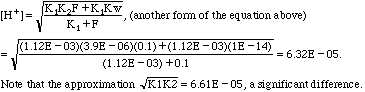
pH = 4.20 (or 4.18 by the approximation--maybe it wasn't so bad after all).
F. 30.0 mL of 0.100 M ammonia is mixed with 20.0 mL of 0.050 M HCl
NH3
|
NH4+
|
HCl
|
Volume
| |
| Initial
|
3.00
|
0
|
1.00
|
50
mL
|
| Final
|
2.00
|
1.00
|
0
|
50
mL
|
Buffer:
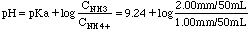
= 9.54
G. 30.0 mL of 0.100 M ammonia is mixed with 40.0 mL of 0.100 M HCl
NH3
|
NH4+
|
HCl
|
Volume
| |
| Initial
|
3.00
|
0
|
4.00
|
70
mL
|
| Final
|
0
|
3.00
|
1.00
|
70
mL
|
Strong Acid (approximation): [H+] ~ CHCl = 1.00mm/70mL = 0.0143 M; pH = 1.85. The NH4+ will contribute little to the H+ because of its very small Ka.
I. 1.3 x 10-4 M benzoic acid.
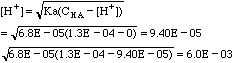
which will go negative on the next iteration. Solve using the quadratic equation.
[H+]2 + Ka[H+] -KaCHA = 0;
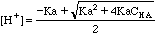 =
6.60E-05 pH = 4.18
=
6.60E-05 pH = 4.18
3. You wish to make a pH 5.00 buffer by adding 6 M HCl to 300 mL of 0.200 M sodium acetate. How many mL of the 6 M HCl will you need to add? Since ionic strength has not been taken into account, how would you then proceed to get the pH adjusted to the right value in a Real World situation?
HA
|
A-
|
HCl
|
Volume
| |
| Initial
|
0
|
60
|
x
|
300
mL + y
|
| Final
|
x
|
60-x
|
0
|
300
mL + y
|
pKa = 4.757, so 5.00 = 4.757 + log ((60-x)/x); x = 21.88 mm or 3.64 mL of 6M HCl
After mixing this buffer, use a pH meter and HCl or NaOH to adjust the pH to exactly 5.00.
4. Calculate the concentration of all carbonate species present if we add 1.00 millimole of sodium carbonate to a solution, then add HCl until the pH is 7.00. The final solution volume was 238 mL. (The carbonate species are H2CO3, HCO3-, and CO32-. We won't worry about how much of the carbonic acid turns into CO2.)
Use the alpha's for carbonate. alpha0 = [H2CO3]/Ct; alpha1 = [HCO3-]/Ct; alpha2 = [CO32-]/Ct
alpha0 = [H+]^2/denom, where denom = [H+]^2 + K1[H+] + K1K2;
alpha0 = 0.1834 after plugging in the K's and 1E-07 for [H+]
alpha1 = [H+]K1/denom = 0.8163
alpha2 = K1K2/denom = 3.828E-04
Ct = 1 mm / 238 mL = 4.20E-03; so [H2A] = (0.1834)(4.20E-03) = 7.7E-04 M; [HA-] = (0.8163)(4.20E-03) = 3.43E-03 M; [A2-] = (3.828E-04)(4.20E-03) = 1.6E-06 M