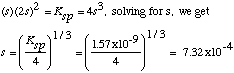105 HE1 F96
Chemistry 105 Hour Exam 1 (Dr. Zellmer)
Gravimetric Analysis, Volumetric Analysis, Statistics and Ksp
Tuesday, October 1, 1996 Morning
100 points (exam sums to 100) Name _________________________________.
Directions: Answer all questions in the spaces provided. Solutions must show
complete set-ups, including units, for credit to be given. Unsupported answers
will be given zero credit. Points may be deducted when improper rounding
causes significant numerical errors. All required values are given on the exam
(plus some extra ones, so choose only what you need). Your calculator and one
3x5 inch card with anything you wish written on it may be brought to the exam.
Additional notes or helps are prohibited.
1. (2 points) Give the molar concentrations for the following Reagent Grade
chemicals as specified in the table given to you in lecture. Your number must
be correct to at least two significant figures.
Hydrochloric Acid
|
12.1 M
|
Ammonia
(Ammonium Hydroxide)
|
14.5 M
|
2. (12 points) 500 mL of an approximately 0.02 M Nitric Acid wash solution is
to be prepared using 6 M nitric acid prepared by diluting the 15 M acid found
in the hood. How many milliliters of the 6 M nitric acid reagent should be
added to the 500 mL of water?
Remember, start with the FINAL solution first. In this case the Final solution
is 500 mL of 0.02 M HNO3. Calculate how many moles of
HNO3 will be required, then calculate the mL of the SOURCE solution
(6 M HNO3) to use. Don't be mislead by other reagents that may be
mentioned in the problem.
0.500 L
|
0.02
mole HNO3
|
L
|
1000
ml
|
|
L
|
6
mole HNO3
|
L
|
= 1.7 mL of 6M HNO3 required.
3. (12 points) You are given an unknown thought to contain 27% Fe. How many
grams of this unknown should you weigh out to get 2.5 millimoles of Fe for a
titration? [GFW of Fe is 55.847.]
Remember the trick of expressing "weird" concentrations units in a way you can
do proper dimensional analysis; e.g. ppm works better as mg/Liter, and 27% Fe
works better as 0.27g Fe/g unk, and GFW of Fe is 55.847 g Fe/mole Fe. We also
should be used to having amounts expressed in millimoles by now, then
converting to grams if we actually have to go into the balance room and weigh
this AMOUNT out. Starting with the millimoles, then
2.5 mmoles Fe
|
1
mole Fe
|
55.847
g Fe
|
g
unknown
|
|
1000
mmole Fe
|
mole
Fe
|
0.27
g Fe
|
= 0.517 g of unknown sample.
4. (12 points) 0.3491 g of an unknown containing chloride is dissolved and
precipitated with 43.89 mL of excess 0.1056 M AgNO3. A sintered
glass crucible weighing 23.4501 g is used to filter out the resulting AgCl.
The new weight of the dried crucible is 23.9622 g. Compute %Cl in the sample.
[GFW's: AgNO3 is 169.837, NaCl is 58.442, AgCl is 143.321, Cl is
35.453.]
A classic error made on problems like this is to somehow assume that "an
unknown containing chloride" is somehow a pure substance that has a formula
weight and everything. Only part of it is chloride. Look to what the problem
is asking you to solve:
%Cl in the sample = (grams Cl/grams sample) x 100%
We HAVE grams of sample; that is 0.3491 grams. Calculating grams of Cl will
take a little more work. The one pure substance we have isolated here is the
AgCl, so we must convert this to the grams of Cl that were in the sample.
23.9622 g (SGC + AgCl) - 23.9622 g (SGC alone) = 0.5121 g AgCl recovered.
The Chemical Reaction is Ag+ + Cl- = AgCl (s).
0.5121 g AgCl
|
mole
AgCl
|
1
mole Cl
|
35.453
g Cl
|
|
143.321
g AgCl
|
1
mole AgCl
|
mole
Cl
|
= 0.12668 g Cl (Remember to use one additonal significant figure for follow-on
calculations. I still see some students rounding to 1 or 2 sig figs in their
calculations. Points are taken off for this, not because of being picky, but
because the final answer will be WRONG.)
Then (0.12668 g Cl/0.3491 g sample) x 100% = 36.29 %Cl (now round to 4 sig
figs).
5. (5 points) In order to save silver nitrate reagent a student decides to
use only about 15 mL of reagent for each titration run in the Chem 105
Volumetric Analysis of Chloride. Also, since the student didn't see why drop
splitting was necessary at the end point, the volumes added could not be
controlled to better than the size of one drop, which is 0.05 mL. Compute the
percent relative error for these titrations, then use this value to explain if
the student is at risk of getting a bad grade. [You are expected to use the
0.2% allowed relative error for the Chloride analysis in your explanation.]
Here it is -- the deadly Relative Error Problem. As explained in lecture on
several occasions, Relative errors are simple errors expressed as a percentage
of the value being measured. In this case we are trying to measure a volume of
about 15 mL. But since our volume change (uncertainty) is a whole 0.05 mL
drop, then
(0.05 mL/15 mL) x 100% = 0.33 % error. Since 0.33 % error is greater than the
0.2% error allowed for the experiment, this is a BAD THING.
The mistake I see consistently on problems of this type is slavish adherence to
a formula that is probably in all of the quant books. It is not wrong, it just
doesn't cover all the cases of relative error we have discussed. The formula
is:

This is a fine equation, but it doesn't apply in this problem because we
already KNOW the uncertainty in our measured value, i.e. 0.05 mL. So don't
look around for true and experimental values here to plug into this equation,
because there are none. (Well -- 15 mL would be the True Value in this case,
but there is no "Experimental Value" as such unless you make one up -- 14.95
and 15.05 would be the extremes of expected experimental values.)
6. Compute the statistics asked for below for the following series of
titrations: 0.0987 M, 0.0973 M, 0.09881 M, 0.0979 M. [For 95% C.L.: t for 1
d.f.= 12.7, 2 d.f. = 4.303, 3 d.f. = 3.18, 4 d.f. = 2.78, 5 d.f. = 2.57 Use
the statistical functions on your calculator. Do NOT take the time to add up
sums of squares "by hand!"]
A. (5 points) Mean
(By calculator) 0.09818 M (An extra significan figure is kept for follow-on
calculations.)
B. (5 points) Standard Deviation
(By calculator) 0.000711 M (A few people still did this by hand. There is no
time for that!)
C. (10 points) 95% Confidence Limit. State the formula and specify all
values used before solving.
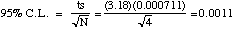
7. 0.3456 g of almost insoluble Ba(IO3)2 is placed in a
beaker with 100.0 mL of water. Ksp Ba(IO3)2 is
1.57x10-9.
A. (5 points) Write the balanced dissociation reaction of
Ba(IO3)2 in water.
Ba(IO3)2 = Ba2+ + 2
IO3-
B. (5 points) Write the Ksp expression for
Ba(IO3)2.
Ksp = [Ba2+][IO3-]2
C. (5 points) Is this a Common Ion, or Simple Solubility Problem?
This is a simple solubility problem. There are no outside sources of
Ba2+ or of IO3-.
D. (10 points) Compute the concentration of IO3- in the
water after the solid barium iodate equilibrates with the water.
For every s moles of Ba(IO3)2 that dissolve, s moles of
Ba2+ and 2s moles of IO3- appear in solution.
There are no other sources of these ions. Plugging into the Ksp expression, we
get
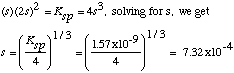
Finally, [IO3-] = 2s = 2 x
7.32x10-4 = 1.46x10-3.
8. (12 points) 0.1000 M AgNO3 is used to precipitate the chloride
in a dissolved unknown. After the reaction, the total volume of the solution
is 155 mL, and an excess of 0.145 millimoles of Ag+ were left over.
Compute the molar concentration of Cl- in the solution.
Ksp AgCl is 1.82x10-10.
This is a Common Ion problem, since 1.45 millimoles of Ag+ are left
over from outside sources. Since you have already been given the final
conditions here, you don't need to spend the time setting up a full
Initial/Final spreadsheet.
CAg+ = [Ag+] (approximately) = 0.145 millimoles/155 mL =
9.35x10-4 M
Then [Cl-] = Ksp/[Ag+] = 1.82x10-10/9.35x10-4
= 1.95x10-7 M