Spectrophotometry and Redox, Part I
Tuesday, November 26, 1996 Afternoon
100 points (exam sums to 90) Name _________Answer Key_________.
Directions: Answer all questions in the spaces provided. Solutions must show complete set-ups, including units, for credit to be given. Unsupported answers will be given zero credit. Points may be deducted when improper rounding causes significant numerical errors. All required values are given on the exam (plus some extra ones, so choose only what you need). Your calculator and one 3x5 inch card with anything you wish written on it may be brought to the exam. Additional notes or helps are prohibited.
The Table of Standard Reduction Potentials that was used in lecture has been attached to this exam. Use this where appropriate on any Redox questions.
1. An unknown containing Fe is to be dissolved, the iron in the sample converted to Fe2+ and then titrated with potassium permanganate (KMnO4) under acid conditions. The potassium permanganate must first be standardized against primary standard sodium oxalate (Na2C2O4) under acid conditions.
A. (10 pts) Using the half reactions found in the attached table, write the full balanced reaction between permanganate and Fe2+.
B. (10 pts) The permanganate is standardized and found to be 0.01534M. 0.9976 grams of unknown iron ore requires 33.47 mL of the permanganate. Compute the %Fe in the unknown. GFWs: Fe is 55.847, Fe2O3 is 159.89, KMnO4 is 158.04, Na2C2O4 is 134.00.MnO4- + 8H+ + 5e- = Mn2+ + 4H20 5 (Fe2+ = Fe3+ + e- )
---------------------------------------------
MnO4- + 5Fe2+ + 8H+ = Mn2+ + 5Fe3+ + 4H20
= 0.1434 g Fe
0.03347 liters
0.01534 moles MnO4- 5 Fe2+ 55.847 g Fe liter 1 MnO4- mole
%Fe = (0.1434 g Fe/0.9976 g unknown)x100% = 14.37 % Fe
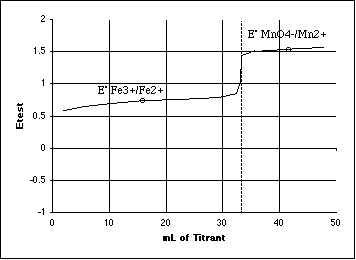
C. (10 pts) Sketch the titration curve for the titration in (B) above. Is the end point predicted to be sharp? Explain, using the Rule given in lecture.

Explain end point sharpness:
The break is approximately 1.51 - 0.771 = 0.739 volts. The Rule states that since
0.739/0.0592 = 12.5, and since 12.5 is much greater than 4, then the break should be sharp.
The warning about this Rule is that in a real titration, the reaction mechanisms involved in a multi-electron transfer may produce a different result than predicted. All we have done is shown that the energy needed for a sharp transition is present. Only a real experiment will tell us if gives us a sharp break or not.
Several students seemed to have forgotten how to "sketch" a redox titration curve. Another common error was forgetting to put the break through the equivalence point milliliters.
Remember that all of our "sketches" allow us to get a quick-and-dirty estimate of what a curve will look like without doing an Initial/Final spreadsheet to compute the potential at each point. For redox reactions we can usually draw the first part of the curve through the Eo of the stuff in the flask, and the last part of the curve through the Eo of the stuff in the buret. Then use the "rule of 4" (in this case change in E/0.0592 should be greater than 4) to estimate the sharpness of the break. This simple sketch could easily be wrong in a redox titration, since pH or the presence of complexing agents can dramatically change the potential of the half reactions.
2. Given the following electrochemical cell:
A. (5 pts) Use the Nernst Equation to calculate the potential on the left.
The balanced half reaction is: Cr2O72- + 14H+ + 6e- = 2Cr3+ + 7H2O
B. (5 pts) Use the Nernst Equation to calculate the potential on the right.
The balanced half reaction is: Hg2Cl2(s) + 2e- = 2Hg + 2 Cl- Eo = 0.268
Eright = 0.268 - (0.0592/2) log[Cl-]2 = 0.268 - (0.0592/2) log[0.100]2 = 0.327 volts
A common error on both parts A and B was making a math error on the calculation itself.
For example, in (B) above: 0.268 - (0.0296)(-2) = 0.268 -(-0.0592) = 0.327, but many people forgot one of the "minuses" and ended up with 0.268 - 0.0592 = 0.209, which is wrong. A similar error happened on part (A).
C. (5 pts) Which electrode will be Negative?
The right (Hg) side.
D. (5 pts) If this cell is used as a Galvanic cell, at which electrode will oxidation take place in the solution?
Electrons are leaving the solution on the negative side of this Galvanic cell so they can flow toward the positive electrode. Loss of electrons is oxidation. So the left side is where oxidation is taking place.
3. A solution is measured on a Spectronic 20 and found to have a %T of 9.6.
A. (5 pts) Compute the Absorbance (A).
A = log (100/%T) = log (100/9.6) = 1.018
B. (5 pts) If Beer's Law is followed, we are using 1.000 cm cells, and the absorptivity has been found to be 2340 micrograms-1 mL cm-1, compute the concentration in micrograms/mL.
A = abC = (2340 micrograms-1 ml cm-1)(1.00 cm) C = 1.018
C = 1.018/2340 = 0.000435 micrograms/ml
C. (10 pts) Is this a "good" absorbance on a Spectronic 20? Explain, stating the practical limits of Absorbance on a Spectronic 20.
The practical limits of absorbance on a Spectronic 20 are between 0.1 and 1.0 absorbance units. A value of 1.018 is only slightly outside of these limits, and still would be OK, since the error function changes fairly slowly. It still would be a good idea to lower the concentration of this sample to get it nearer the 0.3-0.4 minimum on the error function.
A few people said that since the absorbance was not 0.4 it was no good. This is not true. All instrumental methods have some error associated with them. The end user must know the region of acceptable error and be inside of that, but measurements cannot be restricted to the point of minimum error.
4. (10 pts) Which technique has fewer interferences from other compounds in the sample, Atomic Absorbance Spectroscopy (GBC 902), or Molecular Absorbance Spectroscopy (Spectronic 20)? Explain, using a possible absorbance spectrum for each method.
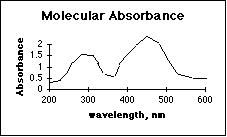
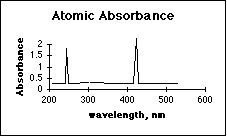
Atomic absorbance has far fewer interferences from other compounds in the sample. The sharp spectral lines in the gas phase (flame) of the AAS make it easy for the monochromator to screen out the lines from unwanted elements.
Many people left this question blank. The presence of working curves drawn on a few of these may indicate confusion as to what a spectrum is. The response of a spectrophotometric instrument over its usable wavelength range is a critical feature of the instrument. Considerable class time was spent discussing this.
5. (10 pts) A dilution scheme calls for dissolving an iron unknown in a 1000 mL volumetric flask (the Stock), taking 50.0 mL of it, putting it in a 500 mL volumetric flask (the Intermediate), then finally diluting 15.0 mL of this in a 50.0 mL flask (the Final). If the concentration in the Final Flask is to be 3.0 micrograms per mL, how much of a 4.6% Fe unknown should we weigh out for the Stock flask?
3.0 microgram Fe
50 mL 500 mL 1000 mL g mL 15 mL 50 mL 106 micrograms = 0.1000 g of Fe
0.1000 g Fe/(0.045 g Fe/g unk) = 2.17 g of unknown.