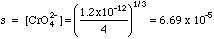
Solubility Product
Sep 19, 1996 Name ____________________________
1. 0.5143 g of Ag2CrO4 is placed in 104.3 mL of water. Ksp of silver chromate is 1.2x10-12.
A. Write the dissociation reaction for silver chromate, then write the Ksp expression for silver chromate.
Ag2CrO4 = 2Ag+ + CrO42-
Ksp = [Ag+]2[CrO42-] = 1.2 x 10-12
B. Calculate the concentrations of Ag+ and of CrO42-.
Since there is no source of silver or of chromate outside of the dissociation of silver chromate itself, this is a simple solubility problem.
From Charge Balance [Ag+] = 2[CrO42-]. Let s = [CrO42-] ; then [Ag+] = 2s . Plugging into the Ksp expression, (2s)2s = Ksp, or 4s3 = Ksp, or s = (Ksp/4)1/3. Putting in the values:
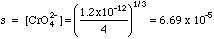
You may need to find out how to take the cube root on your calculator. Look up how to use the yx button.
[Ag+] = 2s = 2(6.69 x 10-5) = 1.34 x 10-4.
2. A solution known to have [Ag+] = 0.045 M has a pile of silver chromate in the bottom of it. Compute the concentration of chromate [CrO42-] in the solution.
Since the [Ag+] has been determined by addition from the outside, probably as AgNO3, this is a common ion problem. From the Ksp expression in problem 1A above, we have:
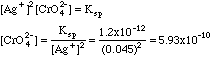
Note that if silver nitrate had been the source of the excess silver, and if the problem had stated that CAg+ = 0.045 M then charge balance would be:
[Ag+] = 2[CrO42-] + [NO3-]
[NO3-] would be large, 0.045 M, but chromate would be very small, about
5.9x10-10 M, so [Ag+] = [NO3-] = 0.045 M to a very good approximation.
3. 100.0 mL of 0.100 M AgNO3 and 50.0 mL of 0.300 M NaCl are mixed together. Complete the following Initial/Final Spreadsheet, finally calculating the concentrations of all species in solution after reaction has taken place. Ksp AgCl is 1.82x10-10.
Balanced Reaction: Ag+ + NO3- + Na+ + Cl- = AgCl(s) + Na+ + NO3-
millimoles
Ag+
|
millimoles
NO3-
|
millimoles
Na+
|
millimoles
Cl-
|
millimoles
AgCl(s)
|
Volumes
| |
| Initial
|
10.0 mmoles
|
10.0 mmoles
|
15.0 mmoles
|
15.0 mmoles
|
none yet
|
100 +
50 mL
|
| Final
|
~0
|
10.0 mmoles
|
15.0 mmoles
|
5.0 mmoles
|
10.0 mmoles
precipitate
|
150 mL
|
| Molar
Conc.
|
5.47x10-9M
|
0.0667 M
|
0.100 M
|
0.0333 M
|
not
in
solution
|
Initial millimoles:
Since AgNO3 ionizes completely in solution ("all nitrates are soluble"),
mmole Ag+ = mmoles NO3- = 100 mL x 0.100 mmole AgNO3/mL = 10.0 mmole Ag+ and NO3-
Since all sodium salts are soluble, NaCl ionizes completely in solution, so
mmole Na+ = mmole Cl- = 50 mL x 0.300 mmole NaCl/mL = 15.0 mmole Na+ and Cl-
Final millimoles:
Silver is the limiting reagent, so it goes to approximately zero.
Chloride is reduced from 15 mmoles to 5 mmoles after the 1:1 reaction with silver.
10.0 mmoles of AgCl(s) are formed as a precipitate that sits at the bottom of the beaker.
The spectator ions remain unchanged.
Final Molar Concentrations:
CNO3- = 10.0 mmoles/150 mL = 0.0667 M
CNa+ = 15.0 mmoles/150 mL = 0.100 M
CCl- = 5.0 mmoles/150 mL = 0.0333 M
then
[Ag+] = Ksp/[Cl-]; appx. = Ksp/CCl- = 1.82x10-10/0.0333 = 5.47x10-9 M (common ion problem)