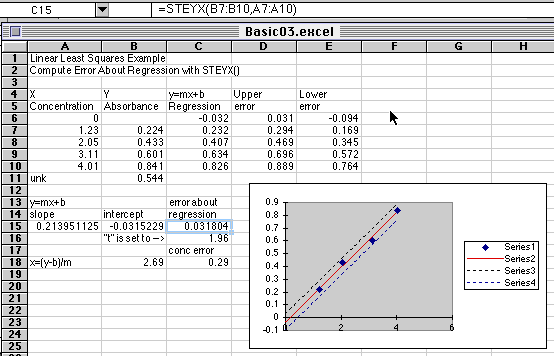
A Basic Working Curve Plot
with Regression Line
and LLS Calculation of Errors using STEYX()
©David L. Zellmer, Ph.D.
Department of Chemistry
California State University, Fresno
A Basic Working Curve Plot |
Last Updated: 8 February 1997