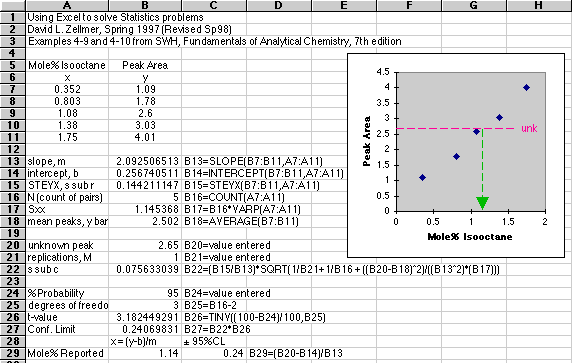
Example 4-9 from Skoog, West and Holler 7th Edition
Computing the Concentration Error from a Working Curve

©David L. Zellmer, Ph.D.
Department of Chemistry
California State University, Fresno

The examples 4-9 and 4-10 from Skoog, West, & Holler, Fundamentals of Analytical Chemistry, 7th edition, could have been worked out exactly as shown in the text, using the spreadsheet to compute all the sums of squares and other values, but knowledge of the statistical functions available on your spreadsheet can save a lot of time. Scroll down to see the figure.
  1. Built-in functions for slope and intercept are common to most spreadsheets. Another way to compute these is using the LINEST() function described elsewhere.

  2. Functions such as the standard deviation about regression, STEYX() may not be common. In this case compute sums of squares and use the more traditional formulas from your book.

  3. Standard deviation STDEV() and mean AVERAGE() are common to most spreadsheets. Values based on the Variance, such as Sxx, can often be computed from the standard deviation, avoiding having to generate additional columns for sums of squares. In this example we used the formula for the Population Variance VARP() which equals Sxx/N.

  4. Finally, we have added a 95% Confidence Limit calculation to the original example. The equation for simple sets of data CL = ts/sqrt(N) is modified here, recognizing that the value s/sqrt(N) is the sc computed from the SWH formula. We need only multiply by Student's t, which is usually looked up from a table. Here we have used the Excel function TINV(probablity,d.f.), where the probabilty is the fraction under one tail of the normal error curve, here 0.05. Degrees of Freedom, d.f., is N-2, since slope and intercept remove TWO degrees of freedom from our five pairs of data.
Return to LLS Basic Master Page
For questions or comments, contact Dr. David Zellmer at david_zellmer@csufresno.edu.

Last Updated: February 16, 1998