
Vol 3. No. 2 (Sep 16, 1998)
Editor: Dr. Larry Cusick.

Erdos was a prolific contributor (over 1500 papers, well over 100 coauthors) to many fields of mathematics, including analysis, probability, number theory, geometry, and combinatorics. He and Selberg discovered an elementary proof of the prime number theorem, and Erdos was among the founders of the fields of random graphs and extremal set theory. He encouraged and has influenced countless young people.
The video manages to convey something of his mathematical interests, his philosophy of, and his unique way of doing mathematics--as well as documenting his eccentricities of lifestyle and language. He traveled constantly; he had no permanent home or job. Erdos would periodically offer monetary awards for the solutions of mathematical problems he thought important. He called children "epsilons'' because the Greek letter is used in mathematics to denote something small (but greater than zero).
Interviews with mathematical collaborators and others who knew Erdos are featured in the video, with English subtitles used for those, including Erdos himself, with heavy accents--even though they are speaking perfectly good English. No mathematical background is required to appreciate the whimsical genius of the man or the major historical, political, and personal events in his lifetime.
--Paul Erdos (1913-1996)
--From Dr. Woo.
Solution to Problem 3.1: The most natural approach to this problem would be double induction. But John Jamison noted that a single induction argument would suffice. Here is his proof.
Let P(m) be the statement "For all n>m, Fn+m + (-1)m Fn-m = LmFn." Using induction on m, the initial step is to prove P(1), which says: for all n>1, Fn+1 - Fn-1 = L1 Fn. This follows immediately from L1 = 1 and the definition of Fn+1.
Now for the inductive step. We assume that there is a k such that P(m) is true for all m less than or equal to k. Let's write out what our inductive assumption is in full: There is a k such that for all m less than or equal to k and for all n>m, Fn+m + (-1)mFn-m = LmFn.
We need to prove that for the above mentioned k, P(k+1) is true, that is: for all n > k+1, Fn+k+1 + (-1)k+1 Fn-k-1 = Lk+1F_n. We do this below: (We use the inductive assumption going from the second line to the third line):
Lk+1Fn = (Lk+Lk-1)Fn
= LkFn + Lk-1Fn
= Fn+k + (-1)k Fn-k + Fn +k+1 + (-1)k-1 Fn-k+1
= Fn = k+1 + (-1)k-1(Fn-k+1 - Fn-k)
= Fn + k+1 + (-1)k+1Fn-k-1}.
Correct solutions were received from Anar Ahmedov, Bryan Chaffe and John Jamison.
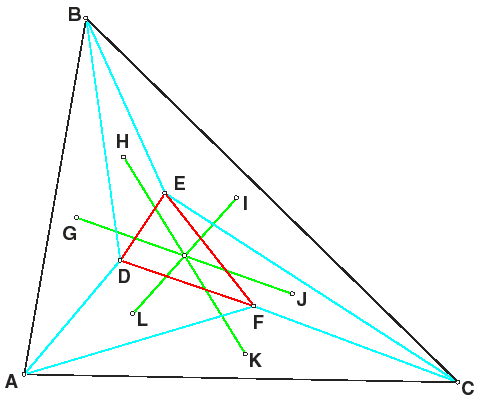
Problem 3.2: (Due Thursday September 24, 3pm) Draw a triangle ABC and a triangle DEF interior to triangle ABC. Let G, H, I, J, K, L be the respective centroids of the triangles (moving clockwise around) triangle ADB, triangle BDE, triangle BEC, triangle CEF, triangle CFA and triangle AFD (see picture below). Prove that the three line segments GJ, HK and IL are concurrent.
Solutions may be delivered to the math department office (for Dr. Cusick) or by e-mail.