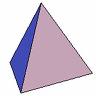
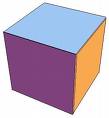
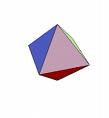
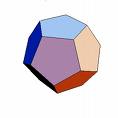
1. (5 points) Determine the number of vertices, the number of edges, and the number of faces (sides) of each of the following solids. Let V, E, and F denote these numbers, respectively. Calculate V-E+F for each solid. This number is called the Euler Characteristic. What do you notice? (We will discuss your results in class.)

2. (5 points) Choose one of the following. (For extra credit: do one or two additional task(s). You can get up to 5 additional points for each additional task.)
A. Explain the result in part 1. Why do you get that number for V-E+F?
B. Make models (e.g. paper or cardboard, or use any other material) of the five Platonic solids. All five models that your group makes must be made of the same material and have the same style.
C. Write a paper explaining why there are only 5 Platonic solids.
D. Make a calendar on a dodecahedron (one month on each face).
E. Find and create an origami project with polyhedra-like shapes.
F. Find (and print out) pictures and/or descriptions of polygons and/or polyhedra found in nature and/or art.
G. Create a piece of art using polygons and/or polyhedra.
H. Think of any other project related to polygons and/or polyhedra (e.g. that you might be able to do with elementary school children).

Platonic solids. A Platonic solid is one whose all sides are congruent (equal) regular polygons and the same number of faces (sides) meet at each vertex. There are five Platonic solids, they are shown below. See also Wikipedia for animated graphics.

• tetrahedron (4 faces, each face is an equilateral triangle, 3 faces meet at each vertex); a tetrahedron is a special case of a triangular pyramid
• cube (6 faces, each face is a square, 3 faces meet at each vertex); a cube is a special case of a rectangular parallelpiped
• octahedron (8 faces, each face is an equilateral triangle, 4 faces meet at each vertex)
• dodecahedron (12 faces, each face is a regular pentagon, 3 faces meet at each vertex)
• icosahedron (20 faces, each face is an equilateral triangle, 5 faces meet at each vertex)

• triangular pyramid (the base is a triangle); a tetrahedron is a special case of a triangular pyramid
• square pyramid (the base is a square)
• rectangular pyramid (the base is a rectangle); a square pyramid is a special case of a rectangular pyramid
• pentagonal pyramid (the base is a pentagon)
• hexagonal pyramid (the base is a hexagon)

• triangular prism (the base is a triangle)
• square prism (the base is a squre); a cube is a special case of a square prism
• rectangular prism, also called a rectangular parallelepiped; a square prism is a special case of a rectanular prism
• pentagonal prism (the base is a pentagon)
• hexagonal prism (the base is a hexagon)