Activity 1. Use the base 10 manipulatives to calculate:

• 254+348
• 348-254

Activity 2. Represent the following problems on a number line.

• 2+4
• 8-3
• 4-5
• -3+5
• -3-5
• 4+(-6)
• -1+(-3)+2+6-5

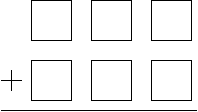
Problem 1. Place the digits 1, 2, 3, 6, 7, and 8 in the boxes below to obtain

(a) the greatest possible sum;
(b) the smallest possible sum.
Explain your strategy!

Problem 2. A group of second grade students are playing the following game. They write digits from 1 to 9 in a row, and put a "+" or a "-" between every two consecutive digits. Then they calculate the result. For example,
1+2+3-4+5+6-7+8-9=5,
1+2-3+4+5-6+7+8-9=9, etc.
The goal is to come up with a sequence of +/- signs for each answer between 1 and 10. (The person who first comes up with 10 sequences, one for each answer, will win.) Is it actually possible to do this?

Problem 3. Modify the game in problem 2 as follows: allow any order of the 9 digits, e.g. 4+8-1+5-7+3+6-2-9. Will your answer to the question in problem 2 change?

Problem 4. What if in the game in problem 2 we allow "combining" two or more consecutive digits, to form two- or more digit numbers. E.g., 123-4-56-7+8-9 will now be allowed. Will your answer to the question in problem 2 change?