Math 100. Exploring Mathematics. Spring 2009.
Project 3: Solids (due May 11)
Work in groups of 3-5 people.
1. Determine the number of vertices, the number of edges, and the number of faces (sides) of each of the following solids. Let V, E, and F
denote these numbers, respectively. Calculate V-E+F for each solid. This number is called the Euler Characteristic. What do you notice? (We will discuss your results in
class.)
| Solid | Vertices | Edges | Faces | V-E+F |
tetrahedron,
triangular pyramid | | | | |
cube,
square prism,
rectangular prism | | | | |
| octahedron | | | | |
| dodecahedron | | | | |
| icosahedron | | | | |
square pyramid,
rectangular pyramid | | | | |
| pentagonal pyramid | | | | |
| hexagonal pyramid | | | | |
| pentagonal prism | | | | |
| hexagonal prism | | | | |
2. Each group will be assigned 3 or 4 solids from the following list. Make a paper (or cardboard) model of each solid assigned to your
group. Label each solid (just write its name on one of the sides).
Platonic solids. A Platonic solid is one whose all sides are congruent (equal) regular polygons. The same number of faces (sides) meet at
each vertex. There are five Platonic solids, they are shown below. See also Wikipedia for animated graphics.
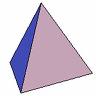
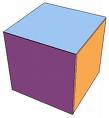
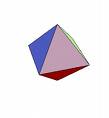
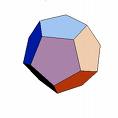

- tetrahedron (4 faces, each face is an equilateral triangle, 3 faces meet at each vertex); a tetrahedron is a special case of a triangular pyramid
- cube (6 faces, each face is a square, 3 faces meet at each vertex); a cube is a special case of a rectangular parallelpiped
- octahedron (8 faces, each face is an equilateral triangle, 4 faces meet at each vertex)
- dodecahedron (12 faces, each face is a regular pentagon, 3 faces meet at each vertex)
- icosahedron (20 faces, each face is an equilateral triangle, 5 faces meet at each vertex)
Pyramids.

- triangular pyramid (the base is a triangle); a tetrahedron is a special case of a triangular pyramid
- square pyramid (the base is a square)
- rectangular pyramid (the base is a rectangle); a square pyramid is a special case of a rectangular pyramid
- pentagonal pyramid (the base is a pentagon)
- hexagonal pyramid (the base is a hexagon)
Prisms.

- triangular prism (the base is a triangle)
- square prism (the base is a squre); a cube is a special case of a square prism
- rectangular prism, also called a rectangular parallelepiped; a square prism is a special case of a rectanular prism
- pentagonal prism (the base is a pentagon)
- hexagonal prism (the base is a hexagon)
Other solids.

- cone (the base is a circle)
- cylinder (the base is a circle)
This page was last revised on 24 March 2008.


















